A commercial airline scheduling cross-training of flight crew between aircraft types.  When flight crew move from one aircraft type to another, they must attend training courses of several weeks before they are ready to fly.  Each individual who is scheduled to move during a year may attend one of a series of appropriate courses subject to their earliest availability date.

The principal objective is to meet staffing requirements as closely as possible throughout the year given the movements of staff in and out of postings.  Since there may be some negotiation involved, the model is able to be re-run with a proportion of the training placements fixed.

Pilots and flight engineers should preferably be trained in "teams" of three (captain, co-pilot, engineer) so that flight simulators can be used efficiently and effectively.  An engineer cannot be trained without at least one pilot.  A pilot may be trained without a pair, but this is highly undesirable if it can be avoided.

The model was originally formulated with an integer variable to count the number of teams on each course, a variable for the number of odd pilots on a course (with a maximum of 1), and a constraint linking them:

The "Fixed pilots" term comes from pilots that are already assigned to the specific course.  Their numbers must be taken into account when assigning the remaining pilots.

Unfortunately, when this model was solved, there were many unpaired pilots in the solution.  The penalty weights on the odd pilot variables dominated the objective value.  As a result, projected staff levels with training on specific aircraft were not close to the required levels.

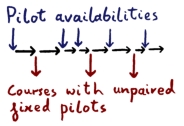
Instead of using optimisation to minimise the number of unpaired pilots, we determine the absolute minimum number of unpaired pilots in each course series by analysis of data.  For each course series, we sort the courses and new availabilities of pilots into date order.  We keep a running total of available pilots and a running total of forced unpaired pilots as we scan this list of events.

If a course has a fixed unpaired pilot then if we have an available pilot we can "fill the hole" – if not then the fixed pilot must remain unpaired.  If we have an odd number of available pilots at the end, then there must be another unpaired pilot at some time during the course series.

In the model we then add a constraint for each course series that forces the total of unpaired pilots to be equal to this calculated minimum.  The penalty weight for unpaired pilots can be removed from the objective function.  There is no need to penalise "missing" engineers either, since minimum unpaired pilots implies minimum number of teams – the number of engineers is fixed, so that implies a minimum number of teams without engineers.

The model now successfully optimises the staff levels and finds better solutions in this respect even though unpaired pilots are more tightly constrained.