Supply chain planning for a manufacturer of polyester yarn.  Please see the "Changeovers" topic for details.  Once the production plan has been developed and agreed, a detailed schedule must be created for the near term.  This is used to directly control operations, steering towards planned production quantities whilst dealing with production upsets and unexpected orders as smoothly as possible.

Clearly the schedule must reflect the production plan, which is the embodiment of a "contract" between sales and operations, as closely as possible.  It must also obey restrictions that allow only certain groups of products to be made together on a line or a group and avoid expensive changeovers as far as possible.  This problem does not fall within the scope of standard scheduling algorithms, so we use mixed integer programming.

The timescale is shorter than for the production plan – typically six weeks rather than one year – but a daily resolution is needed to match production quantities accurately.  The problem is therefore more complex than the production planning model.

There are no interactions between lines once the target production quantities have been defined, so we can solve for one line at a time.  Given the number of lines, each problem has to be solved in a few minutes at the most, which is still challenging. 

We adopt a three-stage approach for each line:

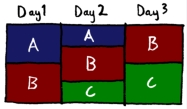
In the first stage, the model is similar to the main production planning model (but for one line only).  Individual positions are not recognised but the number of positions making each product is calculated as a continuous value.  One zero-one variable for each product and day represents the decision to make the product at all, and these are used to enforce the complex constraints on concurrent production.

Only those zero-one decisions from the first stage are kept to use in the second stage model.  This model can then be simplified by leaving out the concurrent production constraints.  The number of positions making each product is defined to be an integral quantity, and the model essentially balances the estimated changeover costs against meeting production targets from the plan.

Having decided how many positions to use for a product in each day, production quantities are determined, and the third stage model no longer needs to be concerned with targets.  Instead products are assigned to specific spinnerets simply to minimise changeovers.  (A small arbitrary bias is introduced to reduce redundancy.)

This three-stage approach is not only faster than a combined model, but finds better solutions in any reasonable amount of time.  Stages 2 and 3 in particular solve very quickly, to a value close or equal to the linear relaxation.