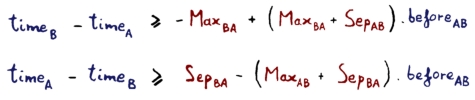Sequencing of flight departures from an airport. Aircraft taking off in sequence from the same runway must obey a collection of minimum time separation rules arising from, for example:

As airline passengers will be aware, flights do not always take off on time, and this is not always due to boarding delays.  The control tower may resequence take-offs (delaying some) in order to maximise the capacity of the runway, subject to the separation rules above, and additional rules:

Optimising the sequence has the potential to increase capacity without the huge expenditure required to build a new runway, for example.

A standard way to tackle a problem of sequencing is to treat it as a variant of the classic travelling salesman problem.  In this instance, the "cities" are flights, and the "distance" between them is the minimum separation time.  The best sequence minimises the distance travelled to visit all the cities (although in this case we do not have to return to the beginning).

There are well-known techniques for tackling the travelling salesman problem, both optimising methods and fast heuristics.  Unfortunately, the take-off time for an aircraft is constrained not only by the time delay after the preceding aircraft, but in principle by all previous aircraft.  A light aircraft may be affected by turbulence from a large passenger jet that took off many minutes earlier.

For each pair of aircraft A and B, we must enforce the rule that if B follows A, then B's take-off time (time_B) must exceed A's take-off time (time_A) by at least some fixed quantity Sep_AB.  If A follows B, then time_A must exceed time_B by at least Sep_BA.  The diagram shows the feasible region (white) which is in two disjoint sections.

This kind of dichotomy is normally handled with a zero-one variable, for example before_AB, which will take a value of 1 if A takes off before B, or 0 otherwise.  The rules defined above can then be represented by the constraints:

where Max_AB is the maximum time A can take off before B, and Max_BA is the maximum time B can take off before A.

This formulation is extremely weak – if Max_AB and Max_BA are large compared to Sep_AB and Sep_BA, then the constraints will have no impact until before_AB is very close to 0 or 1.  At a relaxed optimum, most of the zero-one variables (of which there are many) will take fractional values.  Predictably, the mixed integer solution process is not able to find good solutions in a reasonable amount of time.

The first step is to do as much analysis as possible on earliest and latest take-off times.  In some cases one aircraft must follow another, in which case the before variable can be eliminated and the constraints above simplified to a single linear relationship between the take-off times.  In many cases there is no possibility of one aircraft interacting with another so both the variable and the constraints can be eliminated.

Instead of using binary variables, we define a new kind of discrete constraint – an extension of semi-continuous variables.  A standard semi-continuous variable may take a value of zero or if not zero, then greater than a given conditional minimum.  The extension allows the feasible region to be defined as a series of disjoint ranges.

(The new constraint can be implemented either by modifying the source code of an optimiser or by defining suitable callback routines to an optimiser used in subroutine library form.)

We define a new variable offset_AB as the difference between the take-off times of A and B – negative if A follows B and positive if B follows A, and add a constraint to define its value.  Its feasible region is defined to be:

We can eliminate the constraints defined above.  The linear relaxation for the new problem allows the offset variable to take any value and so is as weak as the original form.  However in most cases there will be no need to branch on the variable – if it takes a value in its feasible region in the relaxed solution, no branching is required.

This modified problem can be solved to an acceptable solution for a whole day of over 600 take-offs.